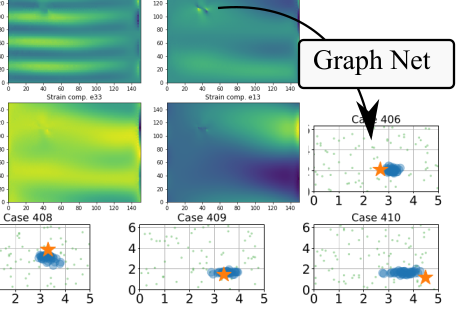
Abstract
A common shortcoming of vibration-based damage localization techniques is that localized damages, i.e. small cracks, have a limited influence on the spectral characteristics of a structure. In contrast, even the smallest of defects, under particular loading conditions, cause localized strain concentrations with predictable spatial configuration. However, the effect of a small defect on strain decays quickly with distance from the defect, making strain-based localization rather challenging. In this work, an attempt is made to approximate, in a fully data-driven manner, the posterior distribution of a crack location, given arbitrary dynamic strain measurements at arbitrary discrete locations on a structure. The proposed technique leverages Graph Neural Networks (GNNs) and recent developments in scalable learning for Bayesian neural networks. The technique is demonstrated on the problem of inferring the position of an unknown crack via patterns of dynamic strain field measurements at discrete locations. The dataset consists of simulations of a hollow tube under random time-dependent excitations with randomly sampled crack geometry and orientation.